
| phone: | E-mail for info |
| e-mail: | harperlangston@gmail.com |
| CV: | M. Harper Langston |
| Github: | https://github.com/harperlangston |
Education
|
PhD in Computer
Science: NYU Courant Institute of Mathematical
Sciences
Dissertation Title:
An Adaptive Fast Volume Solver in Three
Dimensions for Free-Space, Periodic and Dirichlet Boundary
Conditions
Many problems in scientific computing require the accurate and fast solution to a variety of elliptic PDEs. These problems become increasingly dif.cult in three dimensions when forces become non-homogeneously distributed and geometries are complex.
We present an adaptive fast volume solver using a new version of the fast multipole method, incorporated with a pre-existing boundary integral formulation for the development of an adaptive embedded boundary solver.
For the fast volume solver portion of the algorithm, we present a kernel-independent, adaptive fast multipole method of arbitrary order accuracy for solving elliptic PDEs in three dimensions with radiation boundary conditions. The algorithm requires only a Greens function evaluation routine for the governing equation and a representation of the source distribution (the right-hand side) that can be evaluated at arbitrary points.
The performance of the method is accelerated in two ways. First, we construct a piecewise polynomial approximation of the right-hand side and compute far-.eld expansions in the FMM from the coef.cients of this approximation. Second, we precompute tables of quadratures to handle the near-.eld interactions on adaptive octree data structures, keeping the total storage requirements in check through the exploitation of symmetries. We additionally show how we extend the free-space volume solver to solvers with periodic and well as Dirichlet boundary conditions.
For incorporation with the boundary integral solver, we develop interpolation methods to maintain the accuracy of the volume solver. These methods use the existing FMM-based octree structure to locate apppropriate interpolation points, building polynomial approximations to this larger set of forces and evaluating these polynomials to the locally under-re.ned grid in the area of interest.
We present numerical examples for the Laplace, modi.ed Helmholtz and Stokes equations for a variety of boundary conditions and geometries as well as studies of the interpolation procedures and stability of far-.eld and polynomial constructions.
Honors: McCracken Fellowship
Advisors Denis Zorin and
Leslie
Greengard.
|
MS in Scientific
Computing: NYU Courant Institute of Mathematical
Sciences |
Dissertation Title: Investigation
of Computational and Visualization Methods for the Incompressible
Navier-Stokes Equations
Advisors: Denis Zorin, George Biros and Michael Shelley. |
BA
in Mathematics
and Russian: Bowdoin College |
Research Topic: Properties of Non-Unique
Factorization in Quadratic Fields Honors: Smyth Prize in Mathematics, Magna Cum Laude, James Bowdoin Scholor Advisors: Wells Johnson and Adam Levy. |
Publications
 |
Simulations of Future Particle Accelerators: Issues and Mitigations
D. Sagan, M. Berz, N.M. Cook, Y. Hao, G. Hoffstaetter, A. Huebl, C.-K. Huang, M.H. Langston, C.E. Mayes, C.E. Mitchell, C.-K. Ng, J. Qiang, R.D. Ryne, A. Scheinker, E. Stern, J.-L. Vay, D. Winklehner and H. Zhang Journal of Instrumentation (JINST), IOP Publishing, Volume 16, October 2021
The ever increasing demands placed upon machine performance have resulted in the need for more comprehensive particle accelerator modeling. Computer simulations are key to the success of particle accelerators. Many aspects of particle accelerators rely on computer modeling at some point, sometimes requiring complex simulation tools and massively parallel supercomputing. Examples include the modeling of beams at extreme intensities and densities (toward the quantum degeneracy limit), and with ultra-fine control (down to the level of individual particles). In the future, adaptively tuned models might also be relied upon to provide beam measurements beyond the resolution of existing diagnostics. Much time and effort has been put into creating accelerator software tools, some of which are highly successful. However, there are also shortcomings such as the general inability of existing software to be easily modified to meet changing simulation needs. In this paper possible mitigating strategies are discussed for issues faced by the accelerator community as it endeavors to produce better and more comprehensive modeling tools. This includes lack of coordination between code developers, lack of standards to make codes portable and/or reusable, lack of documentation, among others.
|
||||
 |
MACH-B: Fast Multipole Method Approaches in Particle Accelerator Simulations for the Computational and Intensity Frontiers
M. Harper Langston, Julia Wei, Pierre-David Letourneau, Matthew J. Morse, Richard lethin 12th International Particle Accelerator Conference, IPAC'21, Campinas, SP, Brazil, Summer 2021
The MACH-B (Multipole Accelerator Codes for Hadron Beams) project is developing a Fast Multipole Method [1–7] (FMM)-based tool for higher fidelity modeling of particle accelerators for high-energy physics within the next generation of Fermilab’s Synergia simulation package [8]. MACH-B incorporates (1) highly-scalable, high-performance and generally-applicable FMM-based algorithms [5–7, 9] to accurately model space-charge effects in high-intensity hadron beams and (2) boundary integral approaches [10–12] to handle singular effects near the beam pipe using advanced quadratures. MACH-B will allow for more complex beam dynamics simulations that more accurately capture bunch effects and predict beam loss. Further, by introducing an abstraction layer to hide FMM implementation and parallelization complexities, MACH-B removes one of the key impediments to the adoption of FMMs by the accelerator physics community.
|
||||
 |
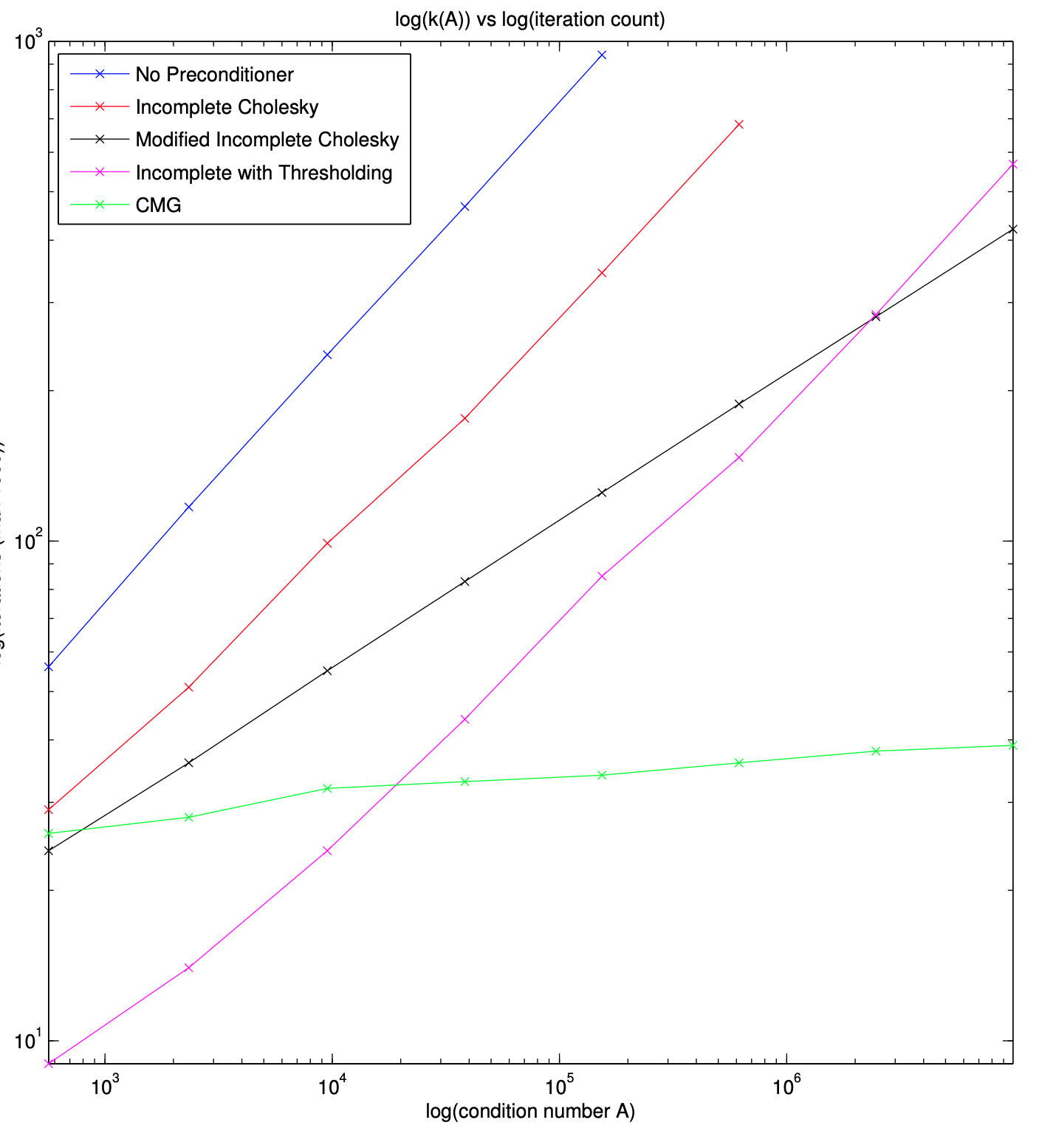
Approximate Inverse Chain Preconditioner: Iteration Count Case Study for Spectral Support Solvers
M. Harper Langston, Pierre-David Letourneau, Julia Wei, Larry Weintraub, Mitchell Harris, Richard Lethin, Eric Papenhausen, Meifeng Lin IEEE High Performance Extreme Computing Conference (HPEC) 2020
As the growing availability of computational power slows, there has been an increasing reliance on algorithmic advances. However, faster algorithms alone will not necessarily bridge the gap in allowing computational scientists to study problems at the edge of scientific discovery in the next several decades. Often, it is necessary to simplify or precondition solvers to accelerate the study of large systems of linear equations commonly seen in a number of scientific fields. Preconditioning a problem to increase efficiency is often seen as the best approach; yet, preconditioners which are fast, smart, and efficient do not always exist.
Following the progress of [1], we present a new preconditioner for symmetric diagonally dominant (SDD) systems of linear equations. These systems are common in certain PDEs, network science, and supervised learning among others. Based on spectra support graph theory, this new preconditioner builds off of the work of [2], computing and applying a V-cycle chain of approximate inverse matrices. This preconditioner approach is both algebraic in nature as well as hierarchically-constrained depending on the condition number of the system to be solved. Due to its generation of an Approximate Inverse Chain of matrices, we refer to this as the AIC preconditioner.
We further accelerate the AIC preconditioner by utilizing precomputations to simplify setup and multiplications in the context of an iterative Krylov-subspace solver. While these iterative solvers can greatly reduce solution time, the number of iterations can grow large quickly in the absence of good preconditioners. Initial results for the AIC preconditioner have shown a very large reduction in iteration counts for SDD systems as compared to standard preconditioners such as Incomplete Cholesky (ICC) and Multigrid (MG). We further show significant reduction in iteration counts against the more advanced Combinatorial Multigrid (CMG) preconditioner.
We have further developed no-fill sparsification techniques to ensure that the computational cost of applying the AIC preconditioner does not grow prohibitively large as the depth of the V-cycle grows for systems with larger condition numbers. Our numerical results have shown that these sparsifiers maintain the sparsity structure of our system while also displaying significant reductions in iteration counts. Keywords: spectral support solver, linear systems, fast solvers, preconditioners, multigrid, graph laplacian, benchmark- ing, iterative solvers, precomputations, approximate inverse chain, sparsifiers, iterative solvers |
||||
 |
Multiscale Data Analysis Using Binning, Tensor Decompositions, and Backtracking
Dimitri Leggas, Thomas S. Henretty, James Ezick, Muthu Baskaran, Brendan von Hofe, Grace Cimaszewski, M. Harper Langston, Richard Lethin IEEE High Performance Extreme Computing Conference (HPEC) 2020
Large data sets can contain patterns at multiple scales
(spatial, temporal, etc.). In practice, it is useful for data exploration
techniques to detect patterns at each relevant scale. In this paper, we
develop an approach to detect activities at multiple scales using
tensor decomposition, an unsupervised high-dimensional data analysis
technique that finds correlations between different features in the data.
This method typically requires that the feature values are discretized
during the construction of the tensor in a process called “binning.”
We develop a method of constructing and decomposing tensors with different
binning schemes of various features in order to uncover patterns across a
set of user-defined scales. While binning is necessary to obtain
interpretable results from tensor decompositions, it also decreases
the specificity of the data. Thus, we develop backtracking methods that
enable the recovery of original source data corresponding to patterns found
in the decomposition. These technique are discussed in the context of
spatiotemporal and network traffic data, and in particular on Automatic
Identification System (AIS) data. Keywords: Tensor Decomposition, Geospatial, Spatiotemporal, Multiscale |
||||
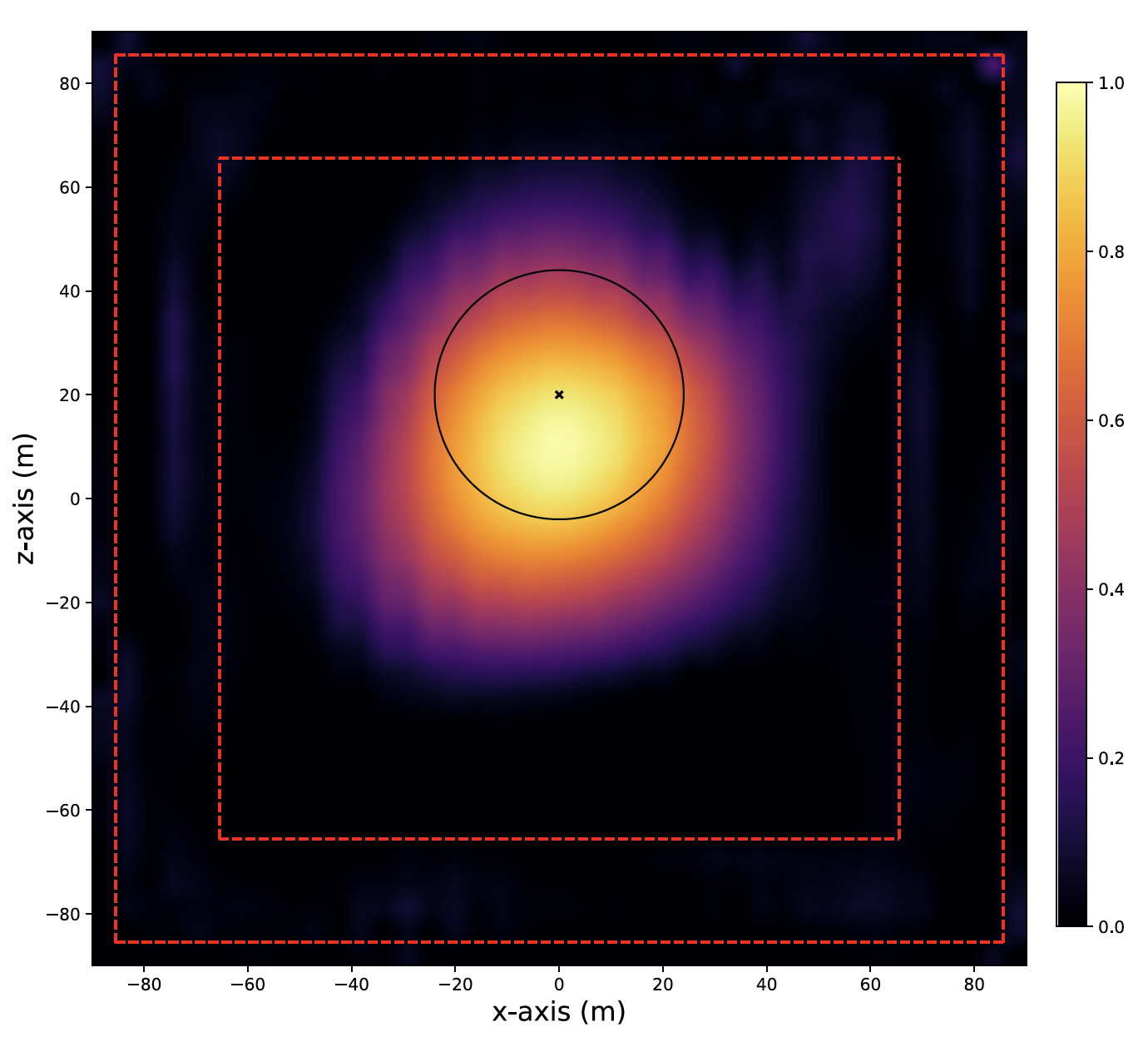 |
Low-Frequency Electromagnetic Imaging Using Sensitivity Functions and
Beamforming
Pierre-David Letourneau, Mitchell Tong Harris, Matthew Harper Langston, and George Papanicolaou SIAM Journal of Imaging Sciences, Vol. 13, No. 2, pp. 807-843, 2020
We present a computational technique for low-frequency electromagnetic imaging in inhomogeneous
media that provides superior three-dimensional resolution over existing techniques. The method
is enabled through large-scale, fast (low-complexity) algorithms that we introduce for simulating
electromagnetic wave propagation. We numerically study the performance of the technique on various
problems including the imaging of a strong finite scatterer located within a thick conductive
box. Keywords: imaging, Maxwell’s equations, low frequency, VLF/ELF, computational imaging AMS subject classifications. 78-04, 65R32, 35H99, 65T50 DOI. 10.1137/19M1279502 |
||||
 |
On the Bottleneck Structure of Congestion-Controlled Networks
Jordi Ros-Giralt, Sruthi Yellamraju, Atul Bohara, M. Harper Langston, Richard Lethin, Yuang Jiang, Leandros Tassiulas, Josie Li, Yuang Tan, Malathi Veeraraghavan ACM SIGMETRICS: International Conference on Measurement and Modeling of Computer System, 2020
In this paper, we introduce the Theory of Bottleneck Ordering, a mathematical framework that reveals the bottleneck
structure of data networks. This theoretical framework provides insights into the inherent topological
properties of a network in at least three areas: (1) It identifies the regions of influence of each bottleneck;
(2) it reveals the order in which bottlenecks (and flows traversing them) converge to their steady state
transmission rates in distributed congestion control algorithms; and (3) it provides key insights into the
design of optimized traffic engineering policies. We demonstrate the efficacy of the proposed theory in TCP
congestion-controlled networks for two broad classes of algorithms: Congestion-based algorithms (TCP BBR)
and loss-based additive-increase/multiplicative-decrease algorithms (TCP Cubic and Reno). Among other
results, our network experiments show that: (1) Qualitatively, both classes of congestion control algorithms
behave as predicted by the bottleneck structure of the network; (2) flows compete for bandwidth only with
other flows operating at the same bottleneck level; (3) BBR flows achieve higher performance and fairness
than Cubic and Reno flows due to their ability to operate at the right bottleneck level; (4) the bottleneck
structure of a network is continuously changing and its levels can be folded due to variations in the flows’
round trip times; and (5) against conventional wisdom, low-hitter flows can have a large impact to the overall
performance of a network. |
||||
 |
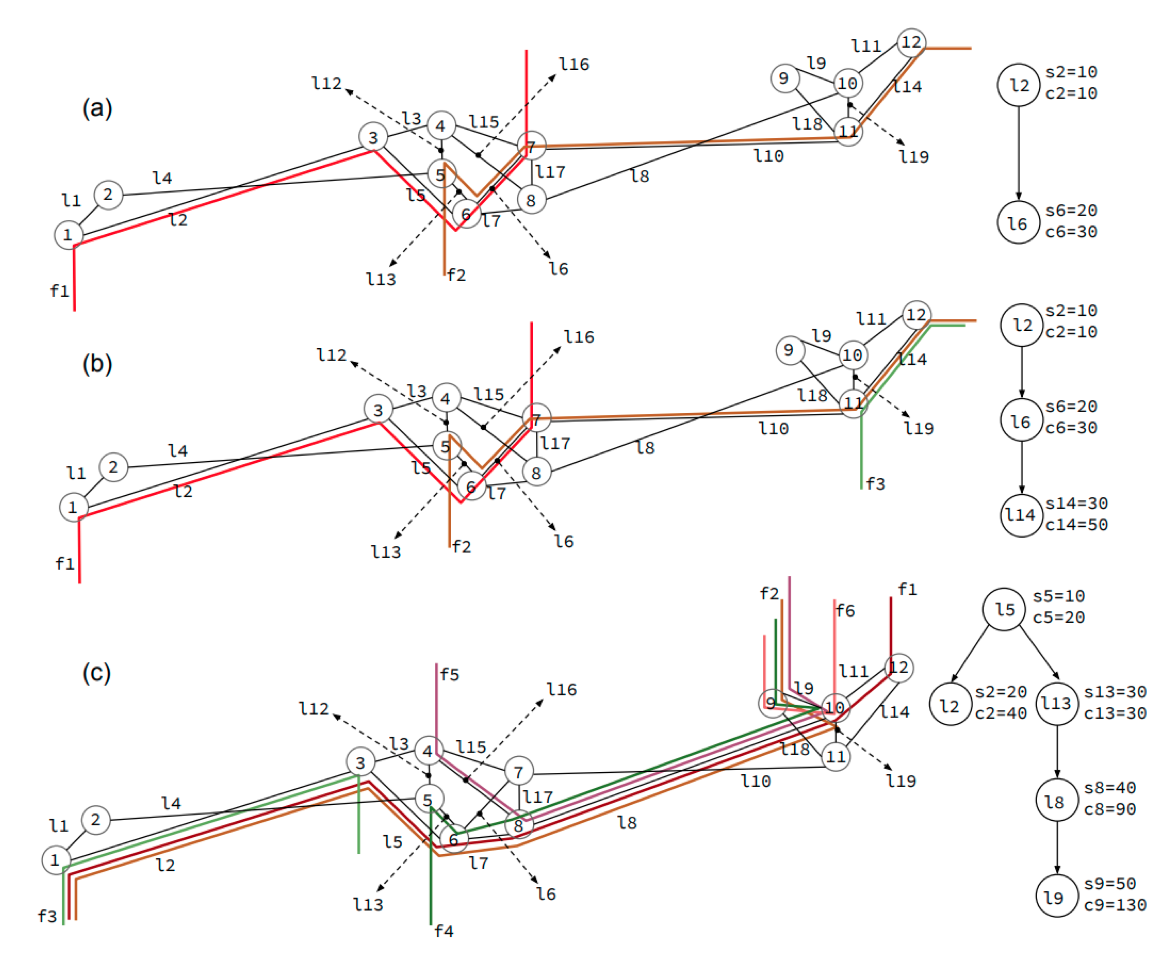
Combinatorial Multigrid: Advanced Preconditioners For Ill-Conditioned Linear
Systems
M. Harper Langston, Mitchell Tong Harris, Pierre-David Letourneau, Richard Lethin, James Ezick IEEE Conference on High Performance Extreme Computing (HPEC '19), 2019.
The Combinatorial Multigrid (CMG) technique is a practical and adaptable solver and combinatorial preconditioner for solving certain classes of large, sparse systems of linear equations. CMG is similar to Algebraic Multigrid (AMG) but replaces large groupings of fine-level variables with a single coarse-level one, resulting in simple and fast interpolation schemes. These schemes further provide control over the refinement strategies at different levels of the solver hierarchy depending on the condition number of the system being solved [1]. While many pre-existing solvers may be able to solve large, sparse systems with relatively low complexity, inversion may require O(n2) space; whereas, if we know that a linear operator has ~n = O(n) nonzero elements, we desire to use O(n) space in order to reduce communication as much as possible. Being able to invert sparse linear systems of equations, asymptotically as fast as the values can be read from memory, has been identified by the Defense Advanced Research Projects Agency (DARPA) and the Department of Energy (DOE) as increasingly necessary for scalable solvers and energy-efficient algorithms [2], [3] in scientific computing. Further, as industry and government agencies move towards exascale, fast solvers and communicationavoidance will be more necessary [4], [5]. In this paper, we present an optimized implementation of the Combinatorial Multigrid in C using Petsc and analyze the solution of various systems using the CMG approach as a preconditioner on much larger problems than have been presented thus far. We compare the number of iterations, setup times and solution times against other popular preconditioners for such systems, including Incomplete Cholesky and a Multigrid approach in Petsc against common problems, further exhibiting superior performance by the CMG. 1 2 Index Terms—combinatorial algorithms, spectral support solver, linear systems, fast solvers, preconditioners, multigrid, graph laplacian, benchmarking, iterative solvers.
|
||||
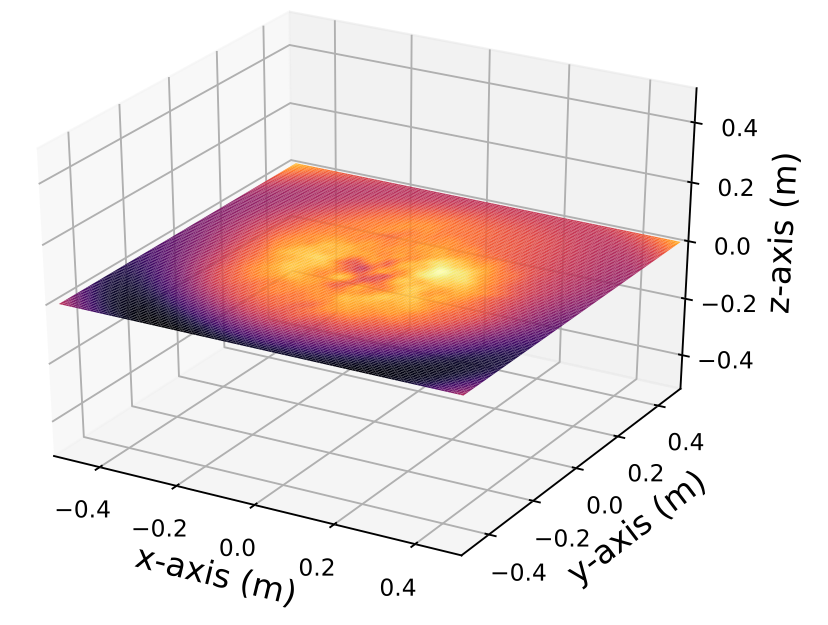 |
Fast Large-Scale Algorithm for Electromagnetic Wave Propagation in 3D Media
Mitchell Tong Harris, M. Harper Langston, Pierre David Letourneau, George Papanicolaou, James Ezick, Richard Lethin IEEE Conference on High Performance Extreme Computing (HPEC '19), 2019.
We present a fast, large-scale algorithm for the simulation of electromagnetic waves (Maxwell’s equations) in three-dimensional inhomogeneous media. The algorithm has a complexity of O(N log(N)) and runs in parallel. Numerical simulations show the rapid treatment of problems with tens of millions of unknowns on a small shared-memory cluster (16 cores).
|
||||
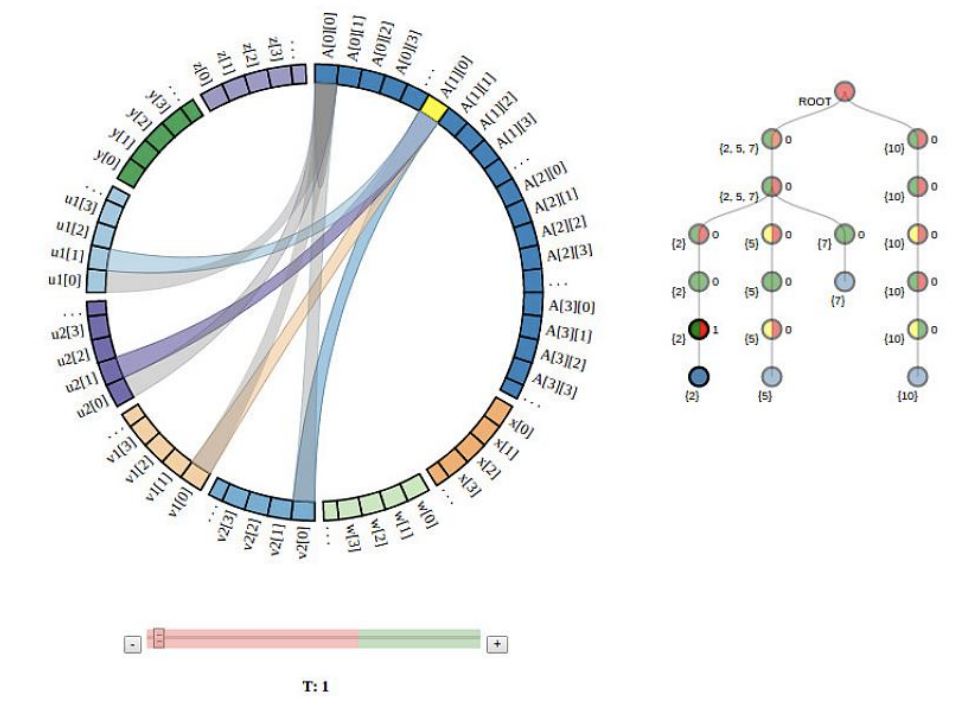 |
PUMA-V: Optimizing Parallel Code Performance Through Interactive Visualization
Eric Papenhause, M. Harper Langston, Benoit Meister, Richard Lethin, Klaus Mueller IEEE Computer Graphics and Applications 39(1): 84-99, 2019
Performance optimization for parallel, loop-oriented
programs compromises between parallelism and
locality. We present a visualization interface which
allows programmers to assist the compiler in
generating optimal code. It greatly improves the
user’s understanding of the transformations that took
place and aids in making additional transformations in
a visually intuitive way.
|
||||
 |
G2: A Network Optimization Framework for High-Precision Analysis of Bottleneck and Flow Performance
Jordi Ros-Giralt, Sruthi Yellamraju, Atul Bohara, Harper Langston, Richard Lethin, Yuang Jiang, Leandros Tassiulas, Josie Li, Ying Lin, Yuanlong Tan, Malathi Veeraraghavan 2019 IEEE/ACM SuperComputing Conference, Innovating the Network for Data-Intensive Science (INDIS) Workshop.
Congestion control algorithms for data networks have been the subject of intense research for the last three decades. While most of the work has focused around the characterization of a flow’s bottleneck link, understanding the interactions amongst links and the ripple effects that perturbations in a link can cause on the rest of the network has remained much less understood. The Theory of Bottleneck Ordering is a recently developed mathematical framework that reveals the bottleneck structure of a network and provides a model to understand such effects. In this paper we present G2, the first operational network optimization framework that utilizes this new theoretical framework to characterize with high-precision the performance of bottlenecks and flows. G2 generates an interactive graph structure that describes how perturbations in links and flows propagate, providing operators new optimization insights and traffic engineering recommendations to help improve network performance. We provide a description of the G2 implementation and a set of experiments using real TCP/IP code to demonstrate its operational efficacy. |
||||
 |
On the Bottleneck Structure of Positive Linear Programming
Jordi Ros-Giralt, Harper Langston, Aditya Gudibanda, Richard Lethin 2019 SIAM Workshop on Network Science.
Positive linear programming (PLP), also known as packing and covering linear programs, is an important class of problems frequently found in fields such as network science, operations research, or economics. In this work we demonstrate that all PLP problems can be represented using a network structure, revealing new key insights that lead to new polynomial-time algorithms.
|
||||
 |
Topic Modeling for Analysis of Big Data Tensor Decompositions
Thomas Henretty, M. Harper Langston, Muthu Baskaran, James Ezick, Richard Lethin SPIE Proceedings Volume 10652, Disruptive Technologies in Information Sciences; 1065208 (2018), doi: 10.1117/12.2306933
Tensor decompositions are a class of algorithms used for unsupervised pattern discovery. Structured, multidimensional datasets are encoded as tensors and decomposed into discrete, coherent patterns captured as weighted collections of high-dimensional vectors known as components. Tensor decompositions have recently shown promising results when addressing problems related to data comprehension and anomaly discovery in cybersecurity and intelligence analysis. However, analysis of Big Data tensor decompositions is currently a critical bottleneck owing to the volume and variety of unlabeled patterns that are produced. We present an approach to automated component clustering and classification based on the Latent Dirichlet Allocation (LDA) topic modeling technique and show example applications to representative cybersecurity and geospatial datasets.v
|
||||
 |
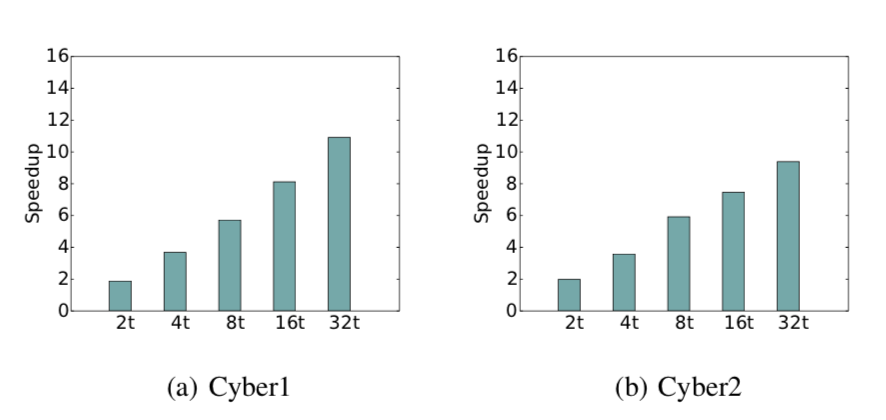
Memory-efficient Parallel Tensor Decompositions
Muthu Baskaran, Tom Henretty, Benoit Pradelle, M. Harper Langston, David Bruns-Smith, James Ezick, Richard Lethin 2017 IEEE High Performance Extreme Computing Conference (HPEC '17), Waltham, MA, USA. [Best Paper Award Winner]
Tensor decompositions are a powerful technique for enabling comprehensive and complete analysis of real-world data. Data analysis through tensor decompositions involves intensive computations over large-scale irregular sparse data. Optimizing the execution of such data intensive computations is key to reducing the time-to-solution (or response time) in real-world data analysis applications. As high-performance computing (HPC) systems are increasingly used for data analysis applications, it is becoming increasingly important to optimize sparse tensor computations and execute them efficiently on modern and advanced HPC systems. In addition to utilizing the large processing capability of HPC systems, it is crucial to improve memory performance (memory usage, communication, synchronization, memory reuse, and data locality) in HPC systems.
In this paper, we present multiple optimizations that are targeted towards faster and memory-efficient execution of large-scale tensor analysis on HPC systems. We demonstrate that our techniques achieve reduction in memory usage and execution time of tensor decomposition methods when they are applied on multiple datasets of varied size and structure from different application domains. We achieve up to 11x reduction in memory usage and up to 7x improvement in performance. More importantly, we enable the application of large tensor decompositions on some important datasets on a multi-core system that would not have been feasible without our optimization. |
||||
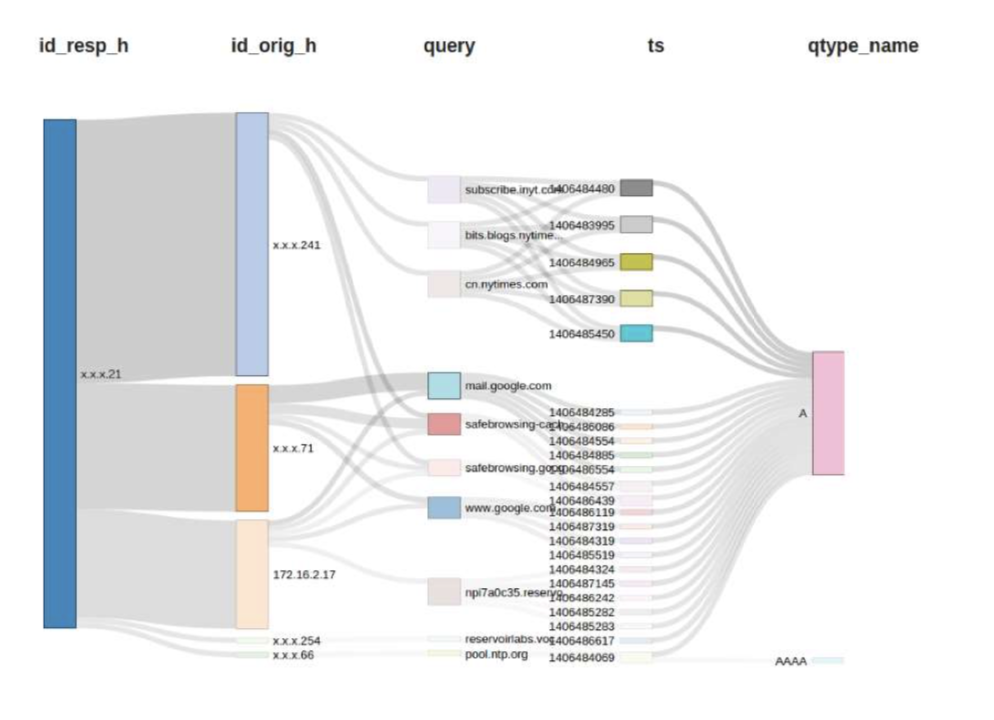 |
Discovering Deep Patterns In Large Scale Network Flows Using Tensor Decompositions
James Ezick, Muthu Baskaran, David Bruns-Smith, Alan Commike, Thomas Henretty, M. Harper Langston, Jordi Ros-Giralt, Richard Lethin FloCon 2017, San Diego, CA
We present an approach to a cyber security workflow based on ENSIGN, a high-performance implementation of tensor decomposition algorithms that enable the unsupervised discovery of subtle undercurrents and deep, cross-dimensional correlations within multi-dimensional data. This new approach of starting from identified patterns in the data complements traditional workflows that focus on highlighting individual suspicious activities. This enhanced workflow assists in identifying attackers who craft their actions to
subvert signature-based detection methods and automates much of the labor intensive forensic process of connecting isolated incidents into a coherent attack profile.
|
||||
| Accelerated Low-rank Updates to Tensor Decompositions Muthu Baskaran, M. Harper Langston, Tahina Ramananandro, David Bruns-Smith, Tom Henretty, James Ezick, Richard Lethin IEEE Conference on High Performance Extreme Computing (HPEC '16), 2016
Tensor analysis (through tensor decompositions) is increasingly becoming popular as a
powerful technique for enabling comprehensive and complete analysis of real-world data.
In many critical modern applications, large-scale tensor data arrives continuously (in streams)
or changes dynamically over time. Tensor decompositions over static snapshots of tensor data become
prohibitively expensive due to space and computational bottlenecks, and severely limit the use of
tensor analysis in applications that require quick response. Effective and rapid streaming
(or non-stationary) tensor decompositions are critical for enabling large-scale real-time analysis.
We present new algorithms for streaming tensor decomposi-tions that effectively use the low-rank structure
of data updates to dynamically and rapidly perform tensor decompositions of continuously evolving data.
Our contributions presented here are integral for enabling tensor decompositions to become a viable analysis
tool for large-scale time-critical applications. Further, we present our newly-implemented parallelized
versions of these algorithms, which will enable more effective deployment of these algorithms in real-world
applications. We present the effectiveness of our approach in terms of faster execution of streaming
tensor decompositions that directly translate to short response time during analysis.
|
||||

| A Sparse Multi-Dimensional Fast Fourier Transform with Stability to Noise in the Context of Image Processing and Change Detection Pierre-David Letourneau, M. Harper Langston, Richard Lethin IEEE Conference on High Performance Extreme Computing (HPEC '16), 2016
We present the sparse multidimensional FFT (sMFFT) for positive real vectors with application to image processing. Our algorithm works in any fixed dimension, requires an (almost) - optimal number of samples
O(Rlog(N/R)) and runs in O(Rlog(N/R)) complexity (to first order) for N unknowns and R nonzeros. It is stable to noise and exhibits an exponentially small probability of failure. Numerical results show sMFFT’s large quantitative and qualitative strengths as compared to
l1-minimization for Compressive Sensing as well as advantages in the context of image processing and change detection.
|
||||
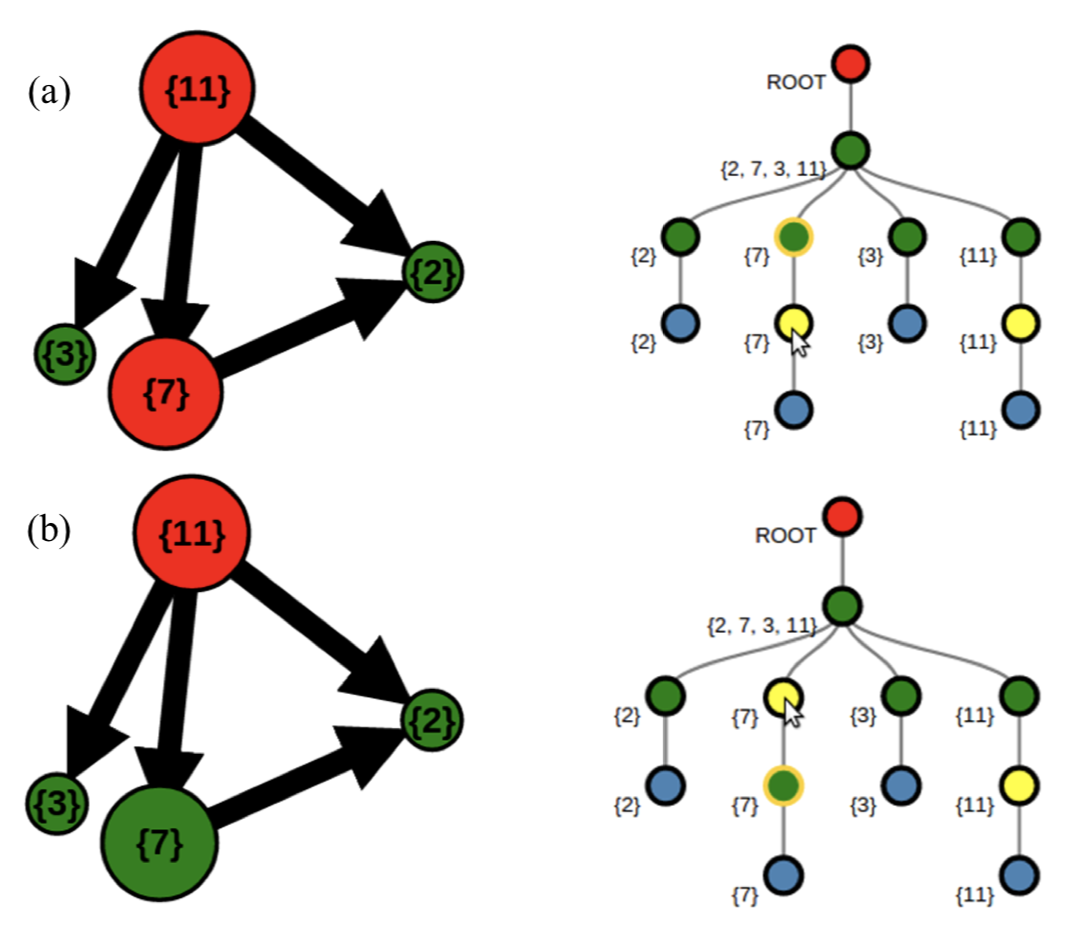 |
An Interactive Visual Tool for Code Optimization and Parallelization Based on the
Polyhedral Model Eric Papenhausen, Klaus Mueller, M. Harper Langston, Benoit Meister, Richard Lethin Sixth International Workshop on Parallel Software Tools and Tool Infrastructures (PSTI 2016), Held in conjunction with ICPP-2016, the 45rd International Conference on Parallel Processing, August 16-19, 2016, Philadelphia, PA
Writing high performance software requires the programmer to take advantage of multi-core processing. This can be done through tools like OpenMP; which allow the programmer to mark parallel loops. Identifying parallelizable loops, however, is a non-trivial task. Furthermore, transformations can be applied to a loop nest to expose parallelism. Polyhedral compilation has become an increasingly popular technique for exposing parallelism in computationally intensive loop nests. These techniques can simultaneously optimize for a number of performance parameters (i.e. parallelism, locality, etc). This is typically done using a cost model designed to give good performance in the general case. For some problems, the compiler may miss optimization opportunities or even produce a transformation that leads to worse performance. In these cases, the user has little recourse; since there are few options for the user to affect the transformation decisions. In this paper we present PUMA-V, a visualization interface that helps the user understand and affect the transformations made by an optimizing compiler based on the polyhedral model. This tool visualizes performance heuristics and runtime performance statistics to help the user identify missed optimization opportunities. Changes to the transformed code can be made by directly manipulating the visualizations. We show an example where performance is greatly improved over the polyhedral model alone by using our tool.
|
||||
 |
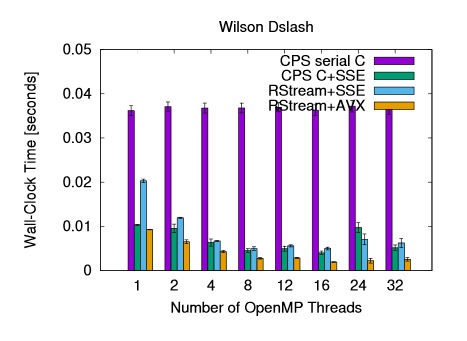
Optimization of the Domain Dslash Operator for Intel Xeon CPUs Meifeng Lin, Eric Papenhausen, M. Harper Langston, Benoit Meister, Muthu Baskaran, Chulwoo Jung, Taku Izubuchi 34th International Symposium on Lattice Field Theory, 2016
In Lattice QCD (LQCD) simulations, the most computation intensive part is the inversion of the fermion Dirac matrix, M. The recurring component of the matrix inversions is the application of the Dirac matrix on a fermion vector. For Wilson fermions, the Dirac matrix can be written as M = 1 − κD, up to a normalization factor, where κ is the hopping parameter, and D is the derivative part of the fermion matrix, the Dslash operator. The matrix-vector multiplication in LQCD essentially reduces to the application of the Dslash operator on a fermion vector. The motivations for this work are to see if source-to-source code generators can produce reasonably performant code if
only given a naive implementation of the Dslash operator as an input;
to investigate optimization strategies in terms of SIMD vectorization, OpenMP
multithreading and multinode scaling with MPI. To produce efficient Dslash code, optimizations in terms of data layout, SIMD, OpenMP scaling and internode communications have been studied.
By vectorizing and changing the memory access pattern, we obtained 34% peak single-core performance in single precision. On single node, OpenMP scaling deteriorates after 16 threads. Multinode strong scaling is limited by the communication cost.
|
||||
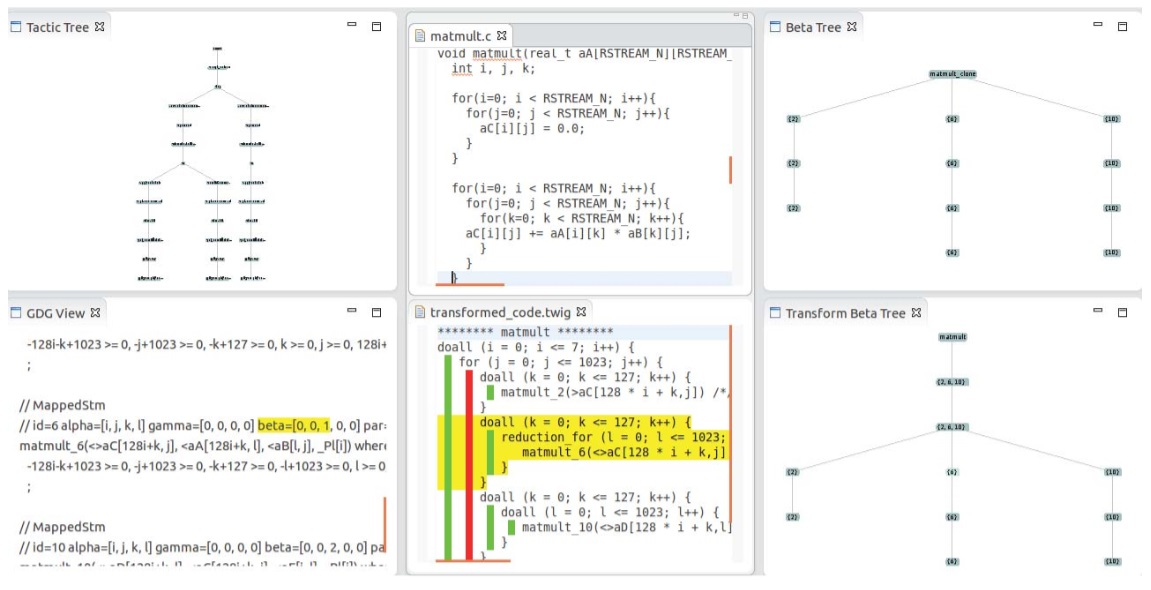 |
Polyhedral User Mapping and Assistant Visualizer
Tool for the R-Stream Auto-Parallelizing Compiler Eric Papenhausen, Bing Wang, Harper Langston, Muthu Baskaran, Tom Henretty, Taku Izubuchi, Ann Johnson, Chulwoo Jung, Meifeng Lin, Benoit Meister, Klaus Mueller, Richard Lethin IEEE 3rd annual Working Conference on Software Visualization (IEEE VISSOFT),Bremen, Germany, IEEE, 2015
Existing high-level, source-to-source compilers can
accept input programs in a high-level language (e.g.,
C
) and
perform complex automatic parallelization and other mappings
using various optimizations. These optimizations often require
trade-offs and can benefit from the user’s involvement in the
process. However, because of the inherent complexity, the barrier
to entry for new users of these high-level optimizing compilers can
often be high. We propose visualization as an effective gateway
for non-expert users to gain insight into the effects of parameter
choices and so aid them in the selection of levels best suited to
their specific optimization goals.
A popular optimization paradigm is polyhedral mapping
which achieves optimization by loop transformations. We have
augmented a commercial polyhedral-model source-to-source
compiler (R-Stream) with an interactive visual tool we call the
Polyhedral User Mapping and Assistant Visualizer (PUMA-V).
PUMA-V is tightly integrated with the R-Stream source-to-source
compiler and allows users to explore the effects of difficult
mappings and express their goals to optimize trade-offs. It
implements advanced multivariate visualization paradigms such
as parallel coordinates and correlation graphs and applies them
in the novel setting of compiler optimizations.
We believe that our tool allows programmers to better
understand complex program transformations and deviations
of mapping properties on well understood programs. This in
turn will achieve experience and performance portability across
programs architectures as well as expose new communities in the
computational sciences to the rich features of auto-parallelizing
high-level source-to-source compilers.
|
||||
 |
Optimizing the domain wall fermion Dirac operator
using the R-Stream source-to-source compiler Meifeng Lin, Eric Papenhausen, M Harper Langston, Benoit Meister, Muthu Baskaran, Taku Izubuchi, Chulwoo Jung 33rd International Symposium on Lattice Field Theory, Kobe International Conference Center, Kobe, Japan, 14 -18 July 2015 The application of the Dirac operator on a spinor field, the Dslash operation, is the most
computation-intensive part of the lattice QCD simulations. It is often the key kernel to optimize
to achieve maximum performance on various platforms. Here we report on a project to optimize
the domain wall fermion Dirac operator in Columbia Physics System (CPS) using the R-Stream
source-to-source compiler. Our initial target platform is the Intel PC clusters. We discuss the
optimization strategies involved before and after the automatic code generation with R-Stream
and present some preliminary benchmark results.
|
||||
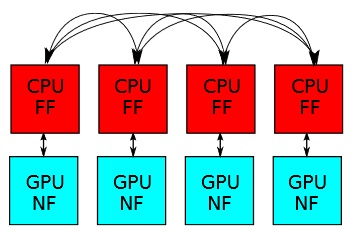 |
Re-Introduction of Communication-Avoiding FMM-Accelerated FFTs with GPU Acceleration M. Harper Langston, Muthu Baskaran, Benoıt Meister, Nicolas Vasilache and Richard Lethin IEEE Conference on High Performance Extreme Computing (HPEC '13) As distributed memory systems grow larger, communication demands have increased. Unfortunately, while the costs of arithmetic operations continue to decrease rapidly, communication costs have not. As a result, there has been a growing interest in communication-avoiding algorithms for some of the classic problems in numerical computing, including communication-avoiding Fast Fourier Transforms (FFTs). A previously-developed low-communication FFT, however, has remained largely out of the picture, partially due to its reliance on the Fast Multipole Method (FMM), an algorithm that typically aids in accelerating dense computations. We have begun an algorithmic investigation and re-implementation design for the FMM-accelerated FFT, which exploits the ability to tune precision of the result (due to the mathematical nature of the FMM) to reduce power-burning communication and computation, the potential benefit of which is to reduce the energy required for the fundamental transform of digital signal processing. We reintroduce this algorithm as well as discuss new innovations for separating the distinct portions of the FMM into a CPU-dedicated process, relying on inter-processor communication for approximate interactions, and a GPU-dedicated process for dense interactions with no communication.
|
||||
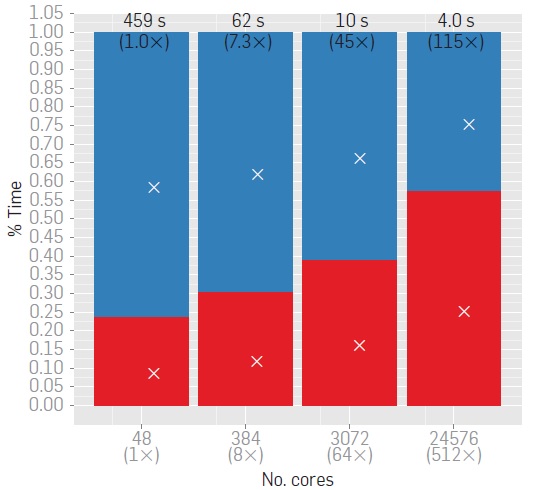 | A
massively parallel adaptive fast-multipole method on
heterogeneous architectures I. Lashuk, A. Chandramowlishwaran, H. Langston, T.-A. Nguyen, R. S. Sampath, A. Shringarpure, R. W. Vuduc, L. Ying, D. Zorin, and G. Biros Communications of the ACM, vol. 55, 5, 2012, pp. 101-109
We describe a parallel fast multipole method (FMM) for
highly nonuniform distributions of particles. We employ both distributed
memory parallelism (via MPI) and shared memory parallelism (via OpenMP
and GPU acceleration) to rapidly evaluate two-body nonoscillatory potentials
in three dimensions on heterogeneous high performance computing architectures.
We have performed scalability tests with up to 30 billion particles on 196,608
cores on the AMD/CRAY-based Jaguar system at ORNL. On a GPU-enabled system
(NSF's Keeneland at Georgia Tech/ORNL), we observed 30x speedup over a single
core CPU and 7x speedup over a multicore CPU implementation. By combining GPUs
with MPI, we achieve less than 10 ns/particle and six digits of accuracy for a
run with 48 million nonuniformly distributed particles on 192 GPUs.
| ||||
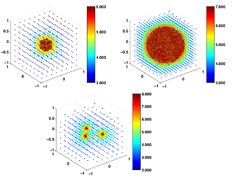 |
A Free-Space Adaptive FMM-Based PDE Solver in
Three Dimensions
H. Langston, L. Greengard, and D. Zorin Communications in Applied Mathematics and Computational Science, vol. 6, no. 1, 2011, pp. 79–122
We present a kernel-independent, adaptive fast
multipole method (FMM) of arbi- trary order
accuracy for solving elliptic PDEs in three
dimensions with radiation and periodic boundary
conditions. The algorithm requires only the
ability to evaluate the Green's function for the
governing equation and a representation of the
source distribution (the right-hand side) that
can be evaluated at arbitrary points. The
performance is accelerated in three ways. First,
we construct a piecewise polynomial
approximation of the right-hand side and compute
far-field expansions in the FMM from the
coefficients of this approximation. Second, we
precompute tables of quadratures to handle the
near-field interactions on adaptive octree data
structures, keeping the total storage
requirements in check through the exploitation
of symmetries. Third, we employ shared-memory
parallelization methods and load-balancing
techniques to accelerate the major algorithmic
loops of the FMM. We present numerical examples
for the Laplace, modified Helmholtz and Stokes equations.
 A
massively parallel adaptive fast-multipole method on
heterogeneous architectures | I. Lashuk, A. Chandramowlishwaran, H. Langston, T.-A. Nguyen, R. S. Sampath, A. Shringarpure, R. W. Vuduc, L. Ying, D. Zorin, and G. Biros Proceedings of SC09 ACM/ICEE SCXY Conference Series, pp. 1-11, 2009, Best Paper Finalist
We present new scalable algorithms and a new
implementation of our kernel-independent fast
multipole method (Ying et al. ACM/IEEE SC '03),
in which we employ both distributed memory
parallelism (via MPI) and shared
memory/streaming parallelism (via GPU
acceleration) to rapidly evaluate two-body
non-oscillatory potentials. On traditional
CPU-only systems, our implementation scales well
up to 30 billion unknowns on 65K cores
(AMD/CRAYbased Kraken system at NSF/NICS) for
highly non-uniform point distributions. We
achieve scalability to such extreme core counts
by adopting a new approach to scalable MPI-based
tree construction and partitioning, and a new
reduction algorithm for the evaluation
phase. Taken together, these components show
promise for ultrascalable FMM in the petascale
era and beyond.
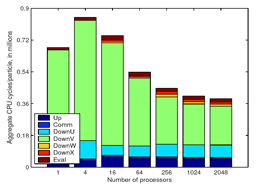 A
New Parallel Kernel-Independent Fast Multipole
Method | L. Ying, G. Biros, H. Langston, and D. Zorin Proceedings of SC03 ACM/ICEE SCXY Conference Series, pp. 1-11, 2003, Best Student Paper, Gordon Bell prize finalist We present a new adaptive
fast multipole algorithm and its parallel
implementation. The algorithm is
kernel-independent in the sense that the
evaluation of pairwise interactions does not rely
on any analytic expansions, but only utilizes
kernel evaluations. The new method provides the
enabling technology for many important problems in
computational science and engineering. Examples
include viscous flows, fracture mechanics and
screened Coulombic interactions. Our MPI-based
parallel implementation logically separates the
computation and communication phases to avoid
synchronization in the upward and downward
computation passes, and thus allows us to fully
exploit computation and communication
overlapping. We measure isogranular and fixed-size
scalability for a variety of kernels on the
Pittsburgh Supercomputing Center's TCS-1
Alphaserver on up to 3000 processors. We have
solved viscous flow problems with up to 2.1
billion unknowns and we have achieved 1.6 Tflops/s
peak performance and 1.13 Tflops/s sustained performance.
|
Selected Technical Reports and Unpublished Manuscripts
| Adaptive
Inhomogeneous PDE Solvers for Complex Geometries H. Langston, L. Greengard, and D. Zorin In Preparation  A sparse multidimensional FFT for real positive vectors
|
Pierre-David Letourneau, M. Harper Langston, Benoit Meister, Richard Lethin In Submission, http://arxiv.org/abs/1604.06682, 2016
We present a sparse multidimensional FFT randomized algorithm (sMFFT) for positive real vectors.
The algorithm works in any fixed dimension, requires an
(almost)-optimal number of samples (O(Rlog(NR))) and runs in O(Rlog(R)log(NR))
complexity (where N is the size of the vector and R the number of nonzeros).
It is stable to noise and exhibits an exponentially small probability of failure.
| ||
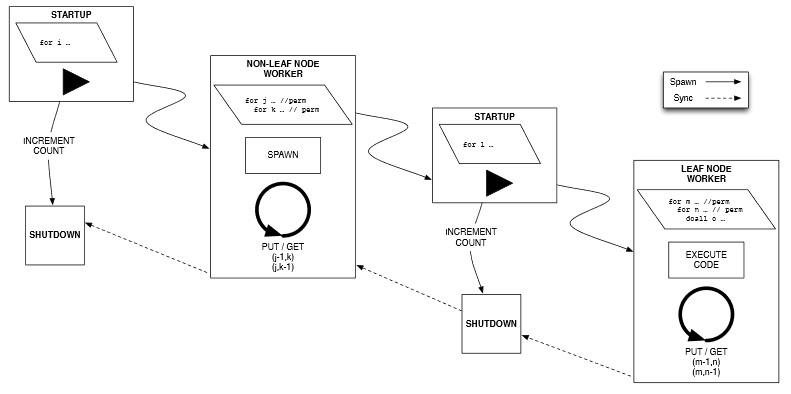 |
A Tale of Three Runtimes Nicolas Vasilache, Muthu Baskaran, Tom Henretty, Benoit Meister, M. Harper Langston, Sanket Tavarageri, Richard Lethin In Submission, 2013 This contribution discusses the automatic generation of event-driven, tuple-space based programs for task-oriented execution models from a sequential C specification. We developed a hierarchical mapping solution using auto-parallelizing compiler technology to target three different runtimes relying on event-driven tasks (EDTs). Our solution benefits from the important observation that loop types encode short, transitive relations among EDTs that are compact and efficiently evaluated at runtime. In this context, permutable loops are of particular importance as they translate immediately into conservative point-to-point synchronizations of distance 1. Our solution generates calls into a runtime-agnostic C++ layer, which we have retargeted to Intel's Concurrent Collections (CnC), ETI's SWARM, and the Open Community Runtime (OCR). Experience with other runtime systems motivates our introduction of support for hierarchical async-finishes in CnC. Experimental data is provided to show the benefit of automatically generated code for EDT-based runtimes as well as comparisons across runtimes.
|
||
 | Avoiding Particle Dissipation for
Adaptive Vortex Methods Through Circulation Conservation H.Langston, Technical Report, 2006
Adaptive fluid solvers have been built in a grid-based fashion,
for which desired areas of refinement must be known beforehand.
This is not always possible, and further, these methods can be
slow for turbulent flows where small time-stepping is required.
Existing vortex methods can address this issue, where vorticity is
transported by particles, causing the non-linear term in the
Navier-Stokes equations to be handled more easily than in grid-based methods
and allowing for better modeling of phenomena such as smoke. Vortex methods
pose additional difficulties, however, in that particles can become clustered,
and resolution can become lost in areas of interest. Voriticity confinement
addresses this loss, but it may lead to unnatural or physically inconsistent
lows. To address the problem of particle dissipation without introducing an
increase in vorticity
field strength, we introduce a method which maintains local circulation
about a closed curve.
 Cash:
Distributed Cooperative Buffer Caching | C. Decoro, H. Langston, J. Weinberger Technical Report, 2004
Modern servers pay a heavy price in block access
time on diskbound workloads when the working set
is greater than the size of the local buffer
cache. We provide a mechanism for cooperating
servers to coordinate and share their local
buffer caches. The coordinated buffer cache can
handle working sets on the order of the
aggregate cache memory, greatly imptoving
performance on diskbound workloads. This
facility is provided with minimal communication
overhead, no penalty for local cache hits, and
without any explicit kernel support.
|
Patents
 |
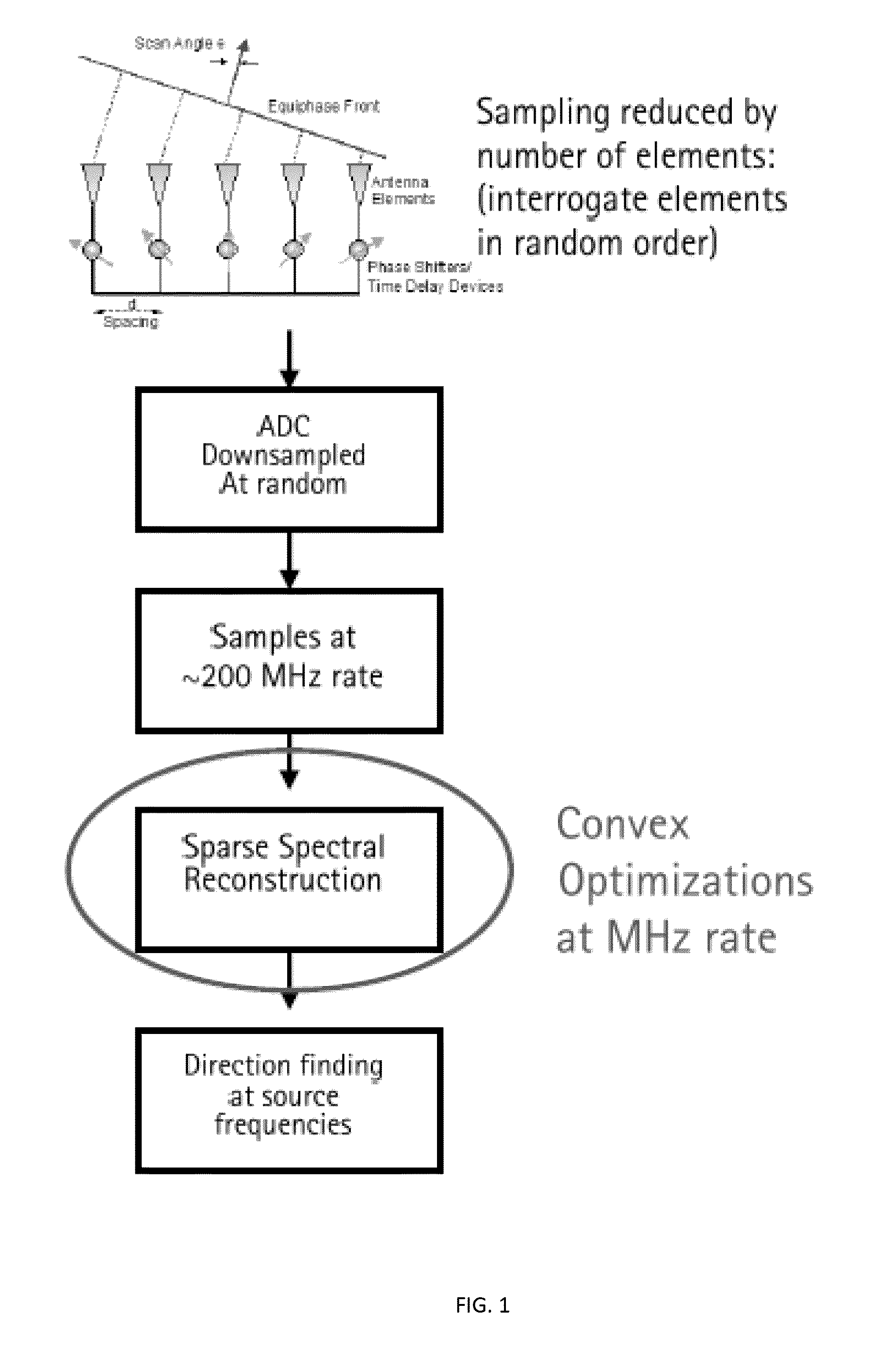
Systems and Methods for Efficient Targeting
Muthu M. Baskaran, Thomas Henretty, Ann Johnson, Athanasios Konstantinidis, M. H. Langston, Janice O. McMahon, Benoit J. Meister, Paul D. Mountcastle, Aale Naqvi, Benoit Pradelle, Tahina Ramananandro, Sanket Tavarageri, Richard A. Lethin November 5, 2019 Publication Source: Patent US10466349B2
A system for determining the physical path of an object can map several candidate paths to a suitable path space that can be explored using a convex optimization technique. The optimization technique may take advantage of the typical sparsity of the path space and can identify a likely physical path using a function of sensor observation as constraints. A track of an object can also be determined using a track model and a convex optimization technique.
|
 |
Systems and Methods for Approximation Based Optimization of Data Processors
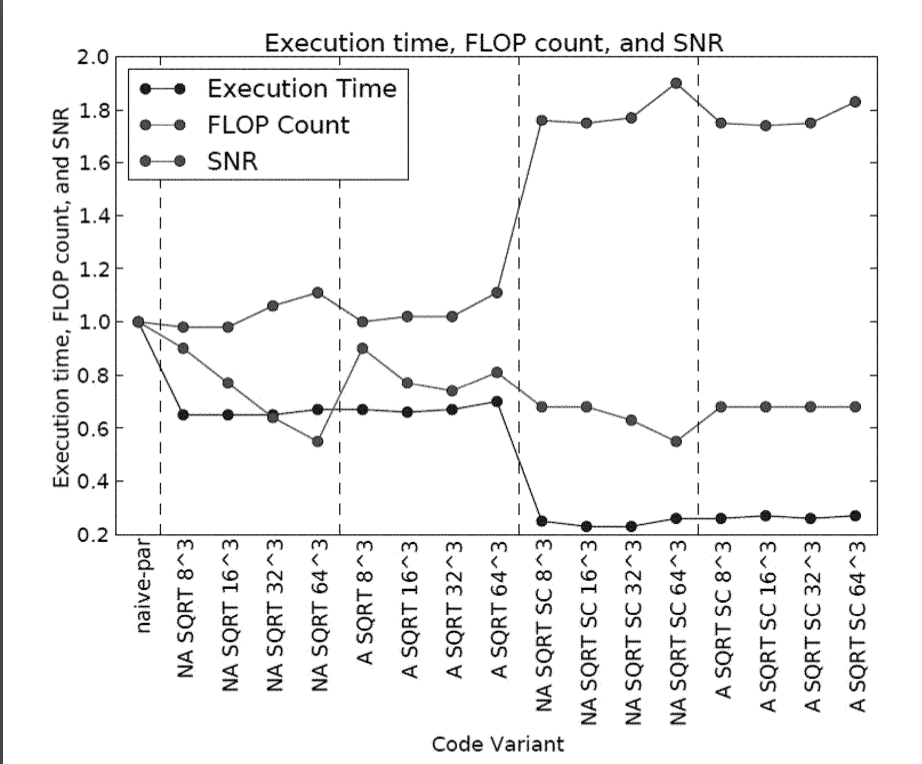
Muthu M. Baskaran, Thomas Henretty, Ann Johnson, Athanasios Konstantinidis, M. H. Langston, Richard A. Lethin, Janice O. McMahon, Benoit J. Meister, Paul Mountcastle February 19, 2019 Publication Source: Patent US10209971B2
A compilation system can apply a smoothness constraint to the arguments of a compute-bound function invoked in a software program, to ensure that the value(s) of one or more function arguments are within specified respective threshold(s) from selected nominal value(s). If the constraint is satisfied, the function invocation is replaced with an approximation thereof. The smoothness constraint may be determined for a range of value(s) of function argument(s) so as to determine a neighborhood within which the function can be replaced with an approximation thereof. The replacement of the function with an approximation thereof can facilitate simultaneous optimization of computation accuracy, performance, and energy/power consumption. |
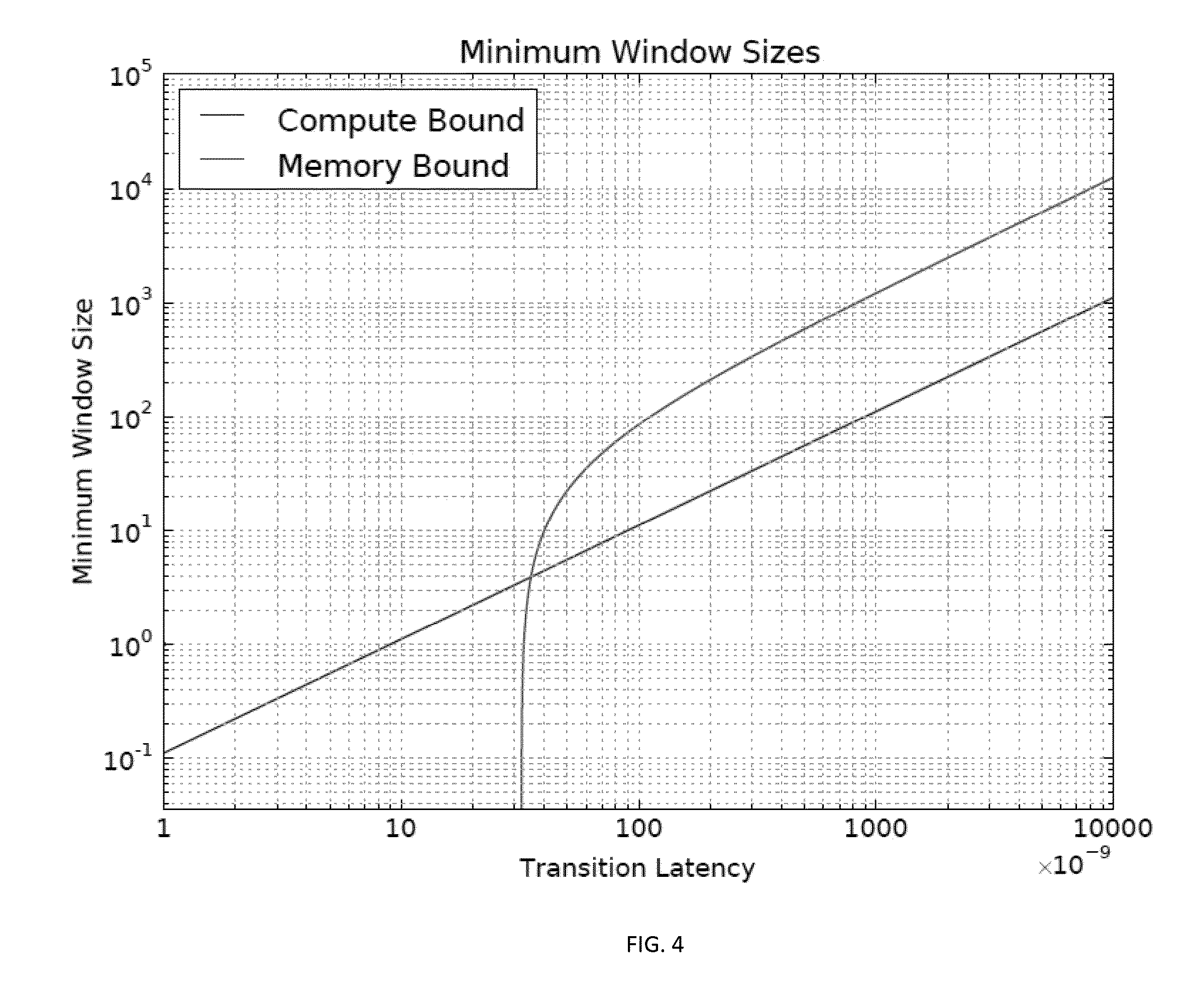 |
Systems and methods for power optimization of processors
Muthu M. Baskaran, Thomas Henretty, Ann Johnson, Athanasios Konstantinidis, M. H. Langston, Richard A. Lethin, Janice O. McMahon, Benoit J. Meister, Paul Mountcastle, Benoit Pradelle January 15, 2019 Publication Source: Patent US20150309779A1
A compilation system generates one or more energy windows in a program to be executed on a data processors such that power/energy consumption of the data processor can be adjusted in which window, so as to minimize the overall power/energy consumption of the data processor during the execution of the program. The size(s) of the energy window(s) and/or power option(s) in each window can be determined according to one or more parameters of the data processor and/or one or more characteristics of the energy window(s).
|
 |
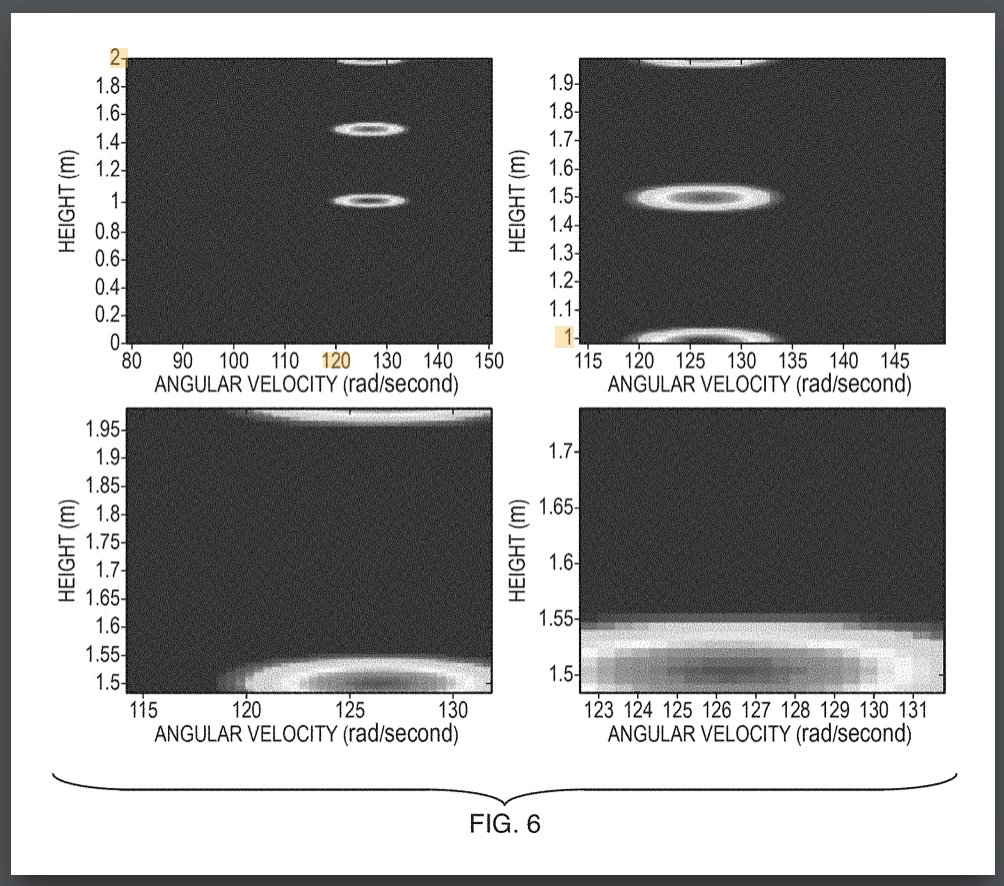
Systems and methods for joint angle-frequency determination
Muthu M. Baskaran, Thomas Henretty, Ann Johnson, M. H. Langston, Richard A. Lethin, Janice O. McMahon, Benoit J. Meister, Paul Mountcastle December 04, 2018 Publication Source: Patent US20150309097A1
A system for data acquisition and processing includes a selector for obtaining samples from one or more sensors, each of which is configured to collect a sample during one or more sampling intervals forming a dwell period. The selector is configured to obtain only a subset of samples of a complete set of samples that can be collected during a dwell period. A solver is configured to solve an underdetermined system based on the collected samples and a mapping relation/phase function, to jointly determine one or more angles and one or more frequencies of transmissions received by the one or more sensors.
|
 |
Systems and Methods for Efficient Determination of Task Dependences After Loop Tiling
Muthu M. Baskaran, Thomas Henretty, Ann Johnson, Athanasios Konstantinidis, M. H. Langston, Janice O. McMahon, Benoit J. Meister, Paul D. Mountcastle, Aale Naqvi, Benoit Pradelle, Tahina Ramananandro, Sanket Tavarageri, Richard A. Lethin October 9, 2018 Publication Source: Patent US9613163B2
A compilation system can compile a program to be executed using an event driven tasks (EDT) system that requires knowledge of dependencies between program statement instances, and generate the required dependencies efficiently when a tiling transformation is applied. To this end, the system may use pre-tiling dependencies and can derive post-tiling dependencies via an analysis of the tiling to be applied.
|
 |
Systems and methods for parallelizing and optimizing sparse tensor computations Muthu M. Baskaran, Thomas Henretty, M. H. Langston, Richard A. Lethin, Benoit J. Meister, Nicolas T. Vasilache October 18, 2016 Publication Source: Patent US9471377B2 A scheduling system can schedule several operations for
parallel execution on a number of work processors. At least one of the operations
is not to be executed, and the determination of which operation or operations are
not to be executed and which ones are to be executed can be made only at run time.
The scheduling system partitions a subset operations that excludes the one or more
operation that are not to be executed into several groups based on, at least in
part, an irregularity of operations resulting from the one or more operation that
are not to be executed. In addition, the partitioning is based on, at least in part,
locality of data elements associated with the subset of
operations to be executed or loading of the several work processors. |